Media, mediana y moda, ejemplos y ejercicios
La media es el valor que se obtiene al sumar todos los datos y dividir el resultado entre la cantidad de datos. La mediana es el valor que ocupa la posición central cuando todos los datos están ordenados en orden creciente o decreciente. La moda es valor que más se repite. Veamos cada una de ellas a detalle con ejemplos y ejercicios
Las medidas de tendencia central, como la media, mediana y moda, son medidas que tratan de ubicar la parte central de un conjunto de datos.
Media (media aritmética)
La media es el valor que se obtiene al sumar todos los datos y dividir el resultado entre la cantidad de datos.
Su fórmula es la siguiente:
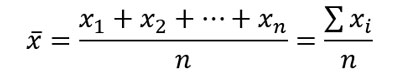Aunque la fórmula parezca complicada, calcular el valor de la media es muy sencillo.
Ejemplo 1
Calcular la media de los siguientes datos: 11, 6, 7, 7, 4.
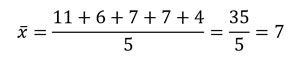
Ejemplo 2
Las edades de 8 niños que van a una fiesta son: 2, 2, 3, 5, 7, 7, 9, 10. Hallar la edad media:
Ejemplo 3
En un examen calificado del 0 al 10, 3 personas obtuvieron 5 de nota, 5 personas obtuvieron 4 de nota, y 2 personas obtuvieron 3 de nota. Calcular la nota media:
Mediana
La mediana es el valor que ocupa la posición central cuando todos los datos están ordenados en orden creciente o decreciente.
La mediana se representa con las letras: Me.
Ejemplo 4
Calcular la mediana de los siguientes datos: 11, 6, 7, 7, 4.
Solución:
Ordenamos los datos de menor a mayor: 4, 6, 7, 7, 11.
Ahora tomamos el dato que se encuentra al centro: 4, 6, 7, 7, 11.
El valor de la mediana es: Me = 7.
¿Y si la cantidad de datos es un número par?
En ese caso, la mediana es la media entre los dos valores centrales.
Ejemplo 5
Calcular la mediana de los siguientes datos: 3, 6, 7, 9, 4, 4.
Solución:
Primero ordenamos los datos de menor a mayor: 3, 4, 4, 6, 7, 9.
La cantidad de datos es 6, es decir, un número par, así que vamos a ubicar los 2 valores centrales: 3, 4, 4, 6, 7, 9.
Entonces, la moda sería la media entre 4 y 6:
Ejemplo 6
En un examen calificado del 0 al 10, 3 personas obtuvieron 5 de nota, 5 personas obtuvieron 4 de nota, y 2 personas obtuvieron 3 de nota. Calcular la mediana.
Solución:
Primero hacemos una lista de las notas obtenidas: 5, 5, 5, 4, 4, 4, 4, 4, 3, 3.
Ahora ordenamos los datos de menor a mayor: 3, 3, 4, 4, 4, 4, 4, 5, 5, 5.
Como el número de datos es par (10), entonces nos enfocamos en los 2 valores centrales: 3, 3, 4, 4, 4, 4, 4, 5, 5, 5.
Finalmente, encontramos la media de estos 2 valores centrales:
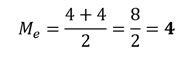
Si al momento de calcular la mediana, ordenas los datos en forma decreciente o descendente, obtendrás el mismo resultado que al hacerlo de forma creciente o ascendente .
Moda
La moda es el valor que más se repite. También podemos decir que la moda es el valor con mayor frecuencia absoluta o el valor que ocurre con más frecuencia.
La moda se representa con las letras: Mo.
Ejemplo 7
Calcular la moda de los siguientes datos: 11, 6, 7, 7, 4.
Podemos ver que el valor que más se repite es el 7, ya que tiene una frecuencia absoluta de 2, por lo tanto, Mo = 7.
Ejemplo 8
En un examen calificado del 0 al 10, 3 personas obtuvieron 5 de nota, 5 personas obtuvieron 4 de nota, y 2 personas obtuvieron 3 de nota. Calcular la moda.
Solución:
Los datos son los siguientes: 5, 5, 5, 4, 4, 4, 4, 4, 3, 3.
El valor que más se repite es el 4, que aparece 5 veces, por lo tanto, Mo = 4.
¿Y si hay varias modas?
Si en un grupo de datos, dos o más valores tienen la misma frecuencia, y es la frecuencia máxima, entonces la distribución tiene dos o más modas y decimos que es bimodal (2 modas), o multimodal (varias modas).
Ejemplo 9
Calcular la moda de los siguientes datos: 3, 4, 4, 6, 7, 7, 9, 11.
Solución:
Como vemos, hay 2 valores que se repiten 2 veces, el 4 y el 7, por lo tanto, los valores de la moda son Mo = 4; 7.
¿Y si todos los valores tienen la misma frecuencia?
Si todos los valores tienen la misma frecuencia, entonces, no hay moda.
Ejemplo 10
Encontrar la moda de los siguientes datos: 3, 3, 5, 5, 6, 6, 7, 7.
Todos los valores tienen una frecuencia de 2, por lo tanto, no hay moda.
Video
A continuación, viene el video que hemos preparado sobre media, mediana y moda con algunos ejemplos y ejercicios resueltos.
EJERCICIOS DE MEDIA, MEDIANA Y MODA
Ejercicio 1
En un consultorio de pediatría, un médico atendió a nueve niños en un día. Midió y registró las alturas de los niños durante las consultas.
| 1.ª consulta | 0,90 m |
|---|---|
| 2.ª consulta | 1,30 m |
| 3.ª consulta | 0,85 m |
| 4.ª consulta | 1,05 m |
| 5.ª consulta | 0,98 m |
| 6.ª consulta | 1,35 m |
| 7.ª consulta | 1,12 m |
| 8.ª consulta | 0,99 m |
| 9.ª consulta | 1,15 m |
Determina la mediana de las alturas de los niños en las consultas.
Ejercicio 2
El gerente de una concesionaria presentó la siguiente tabla en una reunión con directivos. Se sabe que al finalizar la reunión, con el objetivo de elaborar metas y planes para el próximo año, el administrador evaluará las ventas en función de la mediana del número de automóviles vendidos durante el período de enero a diciembre.
| Mes | Número de automóviles vendidos |
|---|---|
| Enero | 25 |
| Febrero | 20 |
| Marzo | 30 |
| Abril | 35 |
| Mayo | 40 |
| Junio | 50 |
| Julio | 45 |
| Agosto | 35 |
| Septiembre | 60 |
| Octubre | 55 |
| Noviembre | 70 |
| Diciembre | 65 |
¿Cuál fue la mediana de los datos presentados?
a) 40,0
b) 42,5
c) 45,0
d) 47,5
e) 50,0
Ejercicio 3
En una eliminatoria para la final de los 100 metros libres de natación en los Juegos Olímpicos, los atletas, en sus respectivos carriles, obtuvieron los siguientes tiempos:
| Carril | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Tiempo | 20,90 | 20,90 | 20,50 | 20,80 | 20,60 | 20,60 | 20,90 | 20,96 |
La mediana de los tiempos presentados en la tabla es:
a) 20,70.
b) 20,77.
c) 20,80.
d) 20,85.
e) 20,90.
Ejercicio 4
Media
Ejercicio 5
La siguiente tabla muestra los precios en las carreras de moto taxi para diferentes barrios de la ciudad de Río de Janeiro, y la cantidad de viajes registrados en un día para cada barrio.
| Barrios | Precio | Número de viajes |
|---|---|---|
| Méier | 20 reales | 3 |
| Madureira | 30 reales | 2 |
| Botafogo | 35 reales | 3 |
| Copacabana | 40 reales | 2 |
Calcula la media de los precios de los viajes en este día.
Ejercicio 6
Analiza el cuadro a continuación.
| 3 | 4 | 4 | 5 | 5 | 7 | 9 |
| 12 | 12 | 21 | 21 | 21 | 21 | 30 |
| 31 | 31 | 31 | 33 | 35 | 42 | 45 |
| 45 | 60 | 72 | 72 | 78 | 89 | 89 |
Marque la opción que presenta la moda de los datos en el cuadro anterior.
a) 9
b) 21
c) 30
d) 30,5
e) 31
Ejercicio 7
Al iniciar sus actividades, un ascensorista registra tanto el número de personas que entran como el número de personas que salen del ascensor en cada uno de los pisos del edificio donde trabaja. El cuadro presenta los registros del ascensorista durante el primer ascenso desde la planta baja, desde donde parten él y otras tres personas, hasta el quinto piso del edificio.
| Número de personas | Planta baja | piso 1 | piso 2 | piso 3 | piso 4 | piso 5 |
|---|---|---|---|---|---|---|
| que entran al ascensor | 4 | 4 | 1 | 2 | 2 | 2 |
| que salen del ascensor | 0 | 3 | 1 | 2 | 0 | 6 |
Basándonos en el cuadro, ¿cuál es la moda del número de personas en el ascensor durante el ascenso desde la planta baja hasta el quinto piso?
a) 2
b) 3
c) 4
d) 5
e) 6
Ejercicio 8
En el verano de 2018, una gran tienda de electrodomésticos registró la cantidad de unidades de ventiladores vendidas durante 10 días consecutivos en la siguiente tabla. Con esto, fue posible verificar el volumen de ventas por día y la variación del número de ventas de un día para el siguiente.
| Día 1 | Día 2 | Día 3 | Día 4 | Día 5 | Día 6 | Día 7 | Día 8 | Día 9 | Día 10 |
| 46 | 53 | 38 | 45 | 49 | 53 | 47 | 47 | 51 | 53 |
¿Cuál es la moda de las variaciones en el número de ventas diarias durante el período considerado?
a) 53
b) 15
c) 7
d) 4
e) 2
EJERCICIOS PRACTICOS Y SENCILLOS
Tema: Moda
Ejercicio 1
Planteamiento del problema:
Un grupo de amigos compara la cantidad de videojuegos que cada uno tiene. Los datos son:
5, 3, 5, 6, 7, 5, 4, 3, 5
Instrucciones:
- Encuentra el número de videojuegos que más se repite en el grupo.
- Escribe el valor de la moda.
Ejercicio 2
Planteamiento del problema:
En una tienda de ropa, los clientes compraron diferentes cantidades de camisetas. Las cantidades vendidas fueron:
2, 4, 3, 4, 5, 2, 4, 4, 3
Instrucciones:
- Observa los datos y determina cuál es la cantidad de camisetas más comprada.
- Escribe el valor de la moda.
Ejercicio 3
Planteamiento del problema:
Los alumnos de una clase registran el número de mascotas que cada uno tiene en casa. Los resultados fueron:
1, 2, 2, 3, 4, 2, 5, 3, 2
Instrucciones:
- Encuentra la cantidad de mascotas que se repite más veces.
- Escribe el valor de la moda.
Tema: Media
Ejercicio 1
Planteamiento del problema:
Un grupo de estudiantes anotó el número de páginas que leyeron en un día. Los resultados son:
12, 15, 10, 8, 20
Instrucciones:
- Suma todas las páginas leídas.
- Divide el total por la cantidad de estudiantes para encontrar la media.
Ejercicio 2
Planteamiento del problema:
Un grupo de cinco niños cuenta cuántas veces fueron al parque en la última semana. Los números son:
3, 4, 2, 5, 6
Instrucciones:
- Suma todas las visitas al parque.
- Divide el total entre 5 para encontrar la media.
Ejercicio 3
Planteamiento del problema:
Los miembros de un equipo de básquetbol anotaron la cantidad de puntos que cada uno hizo en un partido:
14, 18, 12, 10, 16
Instrucciones:
- Suma todos los puntos anotados.
- Divide el total entre la cantidad de jugadores para encontrar la media.
Tema: Mediana
Ejercicio 1
Planteamiento del problema:
Los estudiantes anotaron las edades de sus hermanos. Las edades son:
7, 9, 6, 10, 8
Instrucciones:
- Ordena las edades de menor a mayor.
- Encuentra la edad que está en el medio para hallar la mediana.
Ejercicio 2
Planteamiento del problema:
En un concurso de dibujo, los puntajes obtenidos por los participantes fueron:
5, 7, 6, 9, 8
Instrucciones:
- Ordena los puntajes de menor a mayor.
- Encuentra el valor que está en el centro para hallar la mediana.
Ejercicio 3
Planteamiento del problema:
Un grupo de amigos registró las edades de sus primos. Las edades fueron:
15, 12, 17, 14, 13
Instrucciones:
- Ordena las edades de menor a mayor.
- Encuentra el valor que está en la posición central para hallar la mediana.
No hay comentarios:
Publicar un comentario